Este es un posteo de aprendizaje y de prueba, no debe ser usado como guía técnica y puede estar sujeto a errores.
Monte Carlo
Montecarlo es un casino en Mónaco, el método trae su nombre de ahí.
Con ésto se pueden “estimar” integrales definidas que sean complicadas de calcular, y es un método… “intuitivo” a diferencia de métodos analíticos como las Reglas Gaussianas que no se me ocurrirían jamás.
La idea es “estimar” y no “aproximar” un valor. Valor que veremos viene de un experimento probabilístico.
Como por ejemplo:
¿Cuál es la probabilidad de que al tirar una moneda salga cara?
Bueno podemos tirar la moneda varias veces, vemos cuantas salió cara y dividimos la cantidad de veces que salió cara por la cantidad de veces que la tiramos.
Por ejemplo:
- cantidad de veces que salió cara = 12
- cantidad de veces que tiramos = 20
Llevaremos esta idea durante todo el post, y con un derivado un poco más fuerte de esto calcularemos pi.
Tomemos esta definición primero:
"Una variable aleatoria es el resultado de un fenómeno aleatorio."
Supongamos que el experimento realizado recién, fue un lunes y lo llamamos X1, luego el martes lo llamamos X2, miércoles X3, jueves X4 y viernes X5, así tenemos los 5 experimentos con los distintos valores. Esto es, tenemos cinco variables aleatorias.
Entonces estas variables aleatorias son, la cantiadd de veces que una moneda salió cara, durante cinco días.
Esto se define como X:”Cantidad de veces que salió cara”.
Si sumamos todos esos valores, y los dividimos por la cantidad de experimentos obtendremos el valor esperado del experimento.
Y es algo así por lo que funciona este método.
Más formalmente es:
Esto funciona por que el método se basa en dos grandes resultados:
-
La Ley Fuerte de los Grandes Números.
La idea de esto es que si sumamos todas las variables \(X1+X2+X3+X4+X5\)
Y las dividimos por la cantidad de variables aleatorias
\[\frac{X1+X2+X3+X4+X5}{5}\]Lo que conocemos como promedio, pero de variables aleatorias. Si aumentamos la cantidad de variables mucho, osea
\[\lim_{x\rightarrow ∞} \frac{X1+X2+\dots+Xn}{n}=\mu\]nvariablesEl límite de esto va a ser igual a μ(mu), osea el valor medio de las variables aleatorias.
En criollo si sumamos todos los experimentos y los dividimos por la cantidad de experimentos, el resultado va a ser el valor esperado que tenían esas variables (Como es el límite sería hacer una cantidad enorme de estos experimentos). Hay una condición que no mencioné antes pero X1,X2,X3,X4,X5 tienen que ser independientes y estar idénticamente distribuidas.
-
Un resultado bastante de probabilidad… que no citaré porque no se entiende mucho a priori.
En resumen las dos propiedades nos dicen que es prácticamente improbable que una realización de los experimentos Xs, en nuestro caso X1,X2,X3,X4,X5, no cumpla que el límite de sus promedios se aproxime a un valor estimado θ(Theta) a medida que realizamos más experimentos, osea cuando n tienda a infinito. Esto escrito en fórmula es:
\[\lim_{x\rightarrow ∞} \frac{X1+X2+\dots+Xn}{n}=\theta\]Metamos un ejemplo: Si X1=12, X2=15, X3=13, X4=10, X5=15
Obtendríamos:
\[\frac{12+15+13+10+15}{5}=13\]Entonces tenemos que el número de caras estimado será 13, pero cuanto más valores tengamos, mejor estimaremos el valor.
Estimando π (pi)
Con esta misma noción podemos estimar el valor de π (pi).
Recordemos que el área de un círculo de radio r es π * r², si tomamos r=1, entonces π será calcular el área debajo de la curva de la circunferencia de radio 1 centrada en el punto (x,y)=(0,0)
Formalmente esto se escribe así:
\[\int_{-1}^{1}\int_{-1}^{1}x^2+y^2 dxdy\]Para todos los valores menores a 1 i.e: (x²+y²<1)
En criollo vamos a buscar pares de puntos que caigan dentro de la circunferencia de radio 1, para obtener el valor del área, y así estimar π.
Pero podemos calcular sólo un cuadrante del círculo y luego multiplicarlo por 4.
Entonces tendremos que:
- Sumaremos todos los puntos que cayeron dentro del círculo y los vamos a dividir por la cantidad de puntos que probamos.
Mismo caso que tirar la moneda, sólo contamos las que dieron cara.
Formalmente:
\[4\sum_{j=1}^N {x_j}^2+{y_j}^2 \space ,tales \space que\space (x²+y²<1)\]Esto se lee como “4 por la sumatoria de los xs al cuadrado más los ys al cuadrado, y representa sumar todos los pares que caigan dentro de la circunferencia y multiplicarlos por 4, osea lo mismo para los otros cuadrantes.
Veamos una animación:
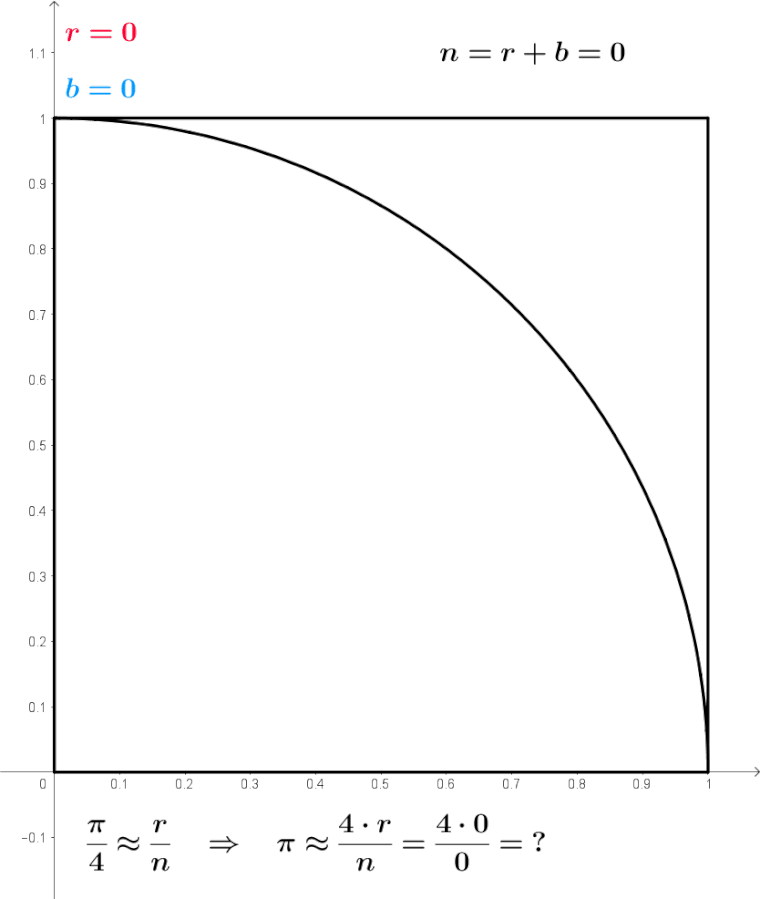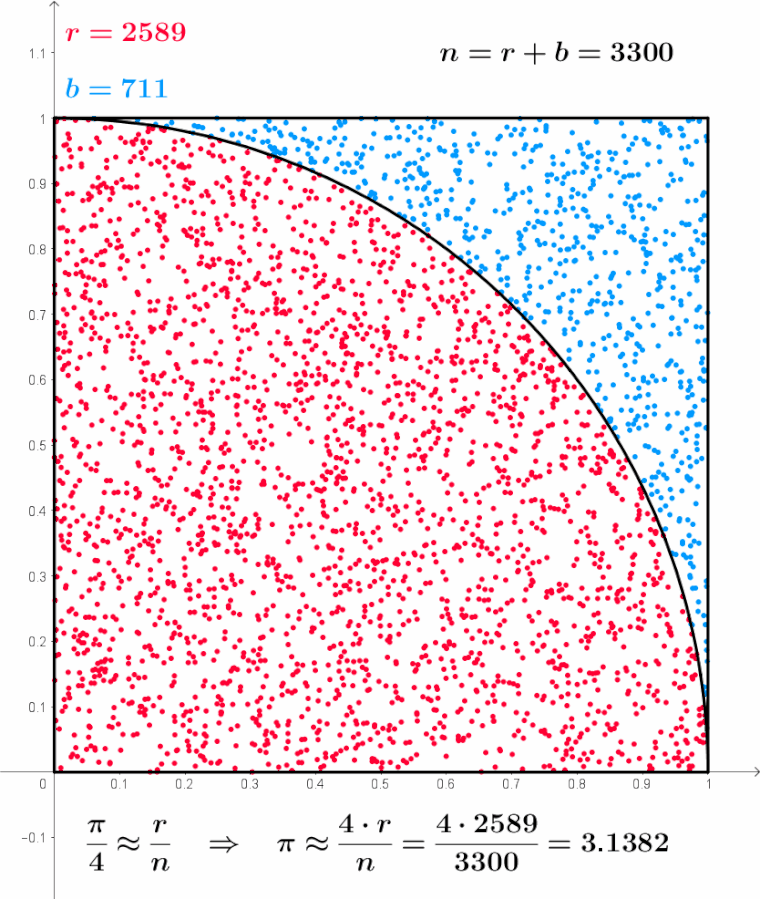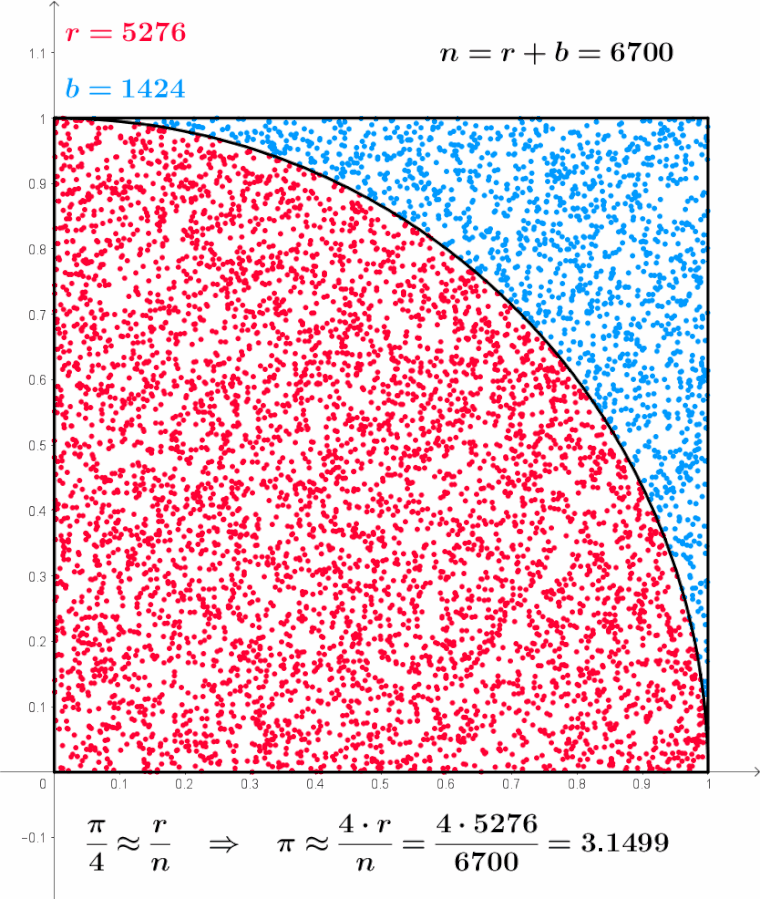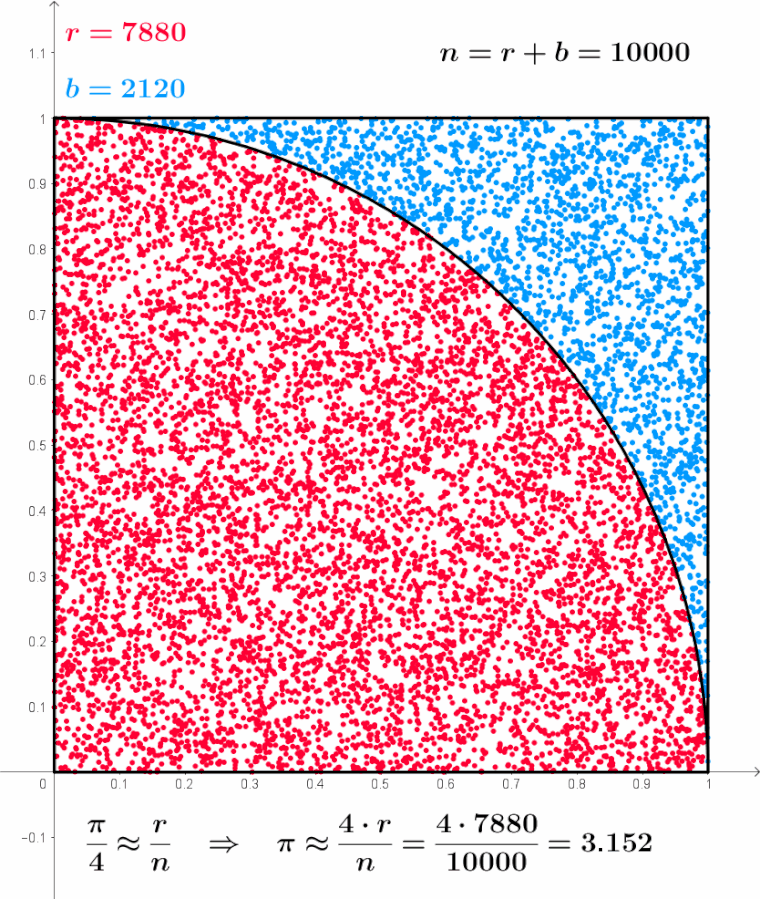
Pensemos qué significa este gif sacado de la Wikipedia.
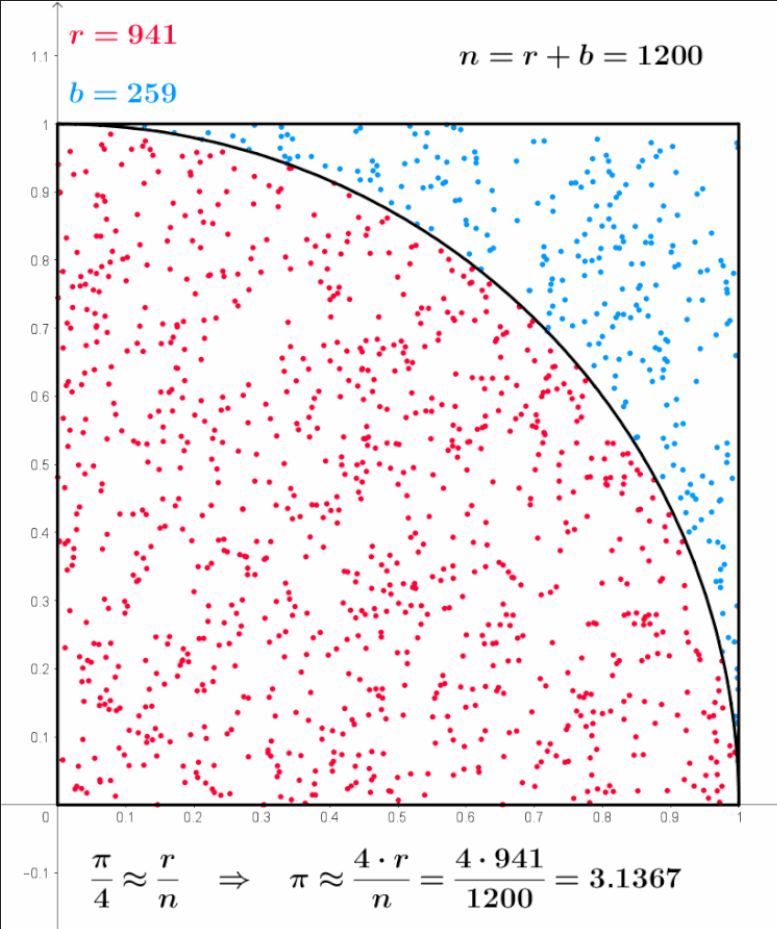Para eso tomamos una foto del gif, veamos que n es la cantidad de puntos total, es la suma de r y de b, osea n=r+b, donde r son los puntos que cayeron dentro de la circunferencia y b los que cayeron fuera de la circunferencia, por eso es que la suma de ambos da 1200:
\(r=941, b=259 \Rightarrow n=r+b=941+259=1200\)
Ahora bien, en el ejemplo inicial de la moneda contábamos la cantidad de caras que nos habían salido y las dividíamos por la cantidad de tiradas que habíamos hecho:
\[\frac{12}{20} \approx 0,6\]Haremos lo mismo con esto la cantidad de puntos que cayeron dentro de la circunferencia la dividiremos por la cantidad de puntos que tiramos.
\[\frac{941}{1200}\approx 0,784166667\]Esto está muy lejos de Pi. Pero esto es sólo para una parte de la circunferencia, recordemos que dijimos:
| “Pero podemos calcular sólo un cuadrante del circulo y luego multiplicarlo por 4.” |
Por lo que ese valor obtenido es sólo un cuadrante de la circunferencia, ahora debemos multiplicar por 4.
\[4*\frac{941}{1200}\approx 3,1367\]Y cuando dijimos que queríamos que n tienda a infinito:
\[\lim_{x\rightarrow ∞}\]Nos referíamos a ir aumentando cada vez más la cantidad de experimentos, de forma tal que si seguimos viendo el gif, el n aumenta hasta 10.000 llegando casi a un valor muy próximo a pi.
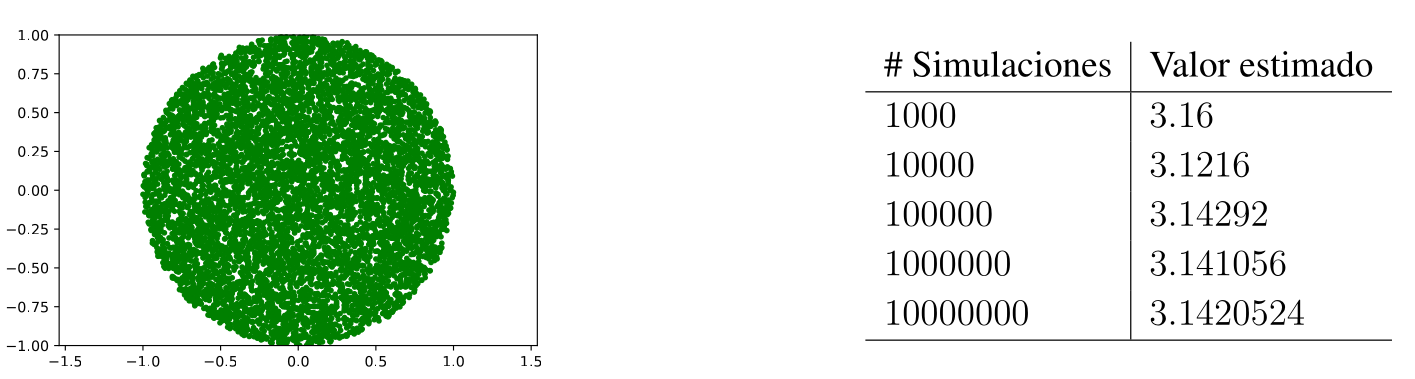
Calculamos un área con una probabilidad… va… no calculamos… estimamos… esa es la principal diferencia de este método, con cualquier método analítico como las Reglas Gaussianas.
Otra de las principales diferencias entre estimar y aproximar, es que la estimación, ósea el método probabilistico que acabamos de ver, nunca habla del error, no tenemos una cota, de error. Por lo general cuando uno aproxima analíticamente, obtiene una fórmula de la aproximación más la fórmula del error, entonces sabe el valor que tiene y por cuánto le está errando. En este caso no podemos saber por cuánto le erramos, porque es una probabilidad.
A mí me pareció increible este método, quizás no está bien explicado, más aún mezclando notación “formal” con querer llevarlo a una forma “sencilla”, hay puntos clave que son omitidos para poder transmitir la idea general.
Dejo código en Python para el cálculo de pi
def valorPi(Nsim):
enCirculo = 0.
for _ in range(Nsim):
u = 2 * random() -1
v = 2 * random() - 1
if u ** 2 + v ** 2 <= 1:
enCirculo += 1
return 4 * enCirculo/Nsim
valorPi(Nsim)